Trigonometry Function Family
'Produce beautiful images using trigonometric graphs.'
The main part of this activity is to produce lovely images like the one on the left. To do that you will need to recognise the patterns behind these graphs. The secret lies in the transformations of functions which hopefully you will know a little about. As a warm up there are a couple of applets which will remind you how to translate a graph and how to stretch it. Once you are comfortable with this you can attempt to produce the beautiful graphs that appear lower down the page. You will probably need some help getting started with Geogebra to produce the graphs, so a help video is included at the bottom of the page. Teachers may wish to refer to the following 
Teacher Notes to find out how to get the best out of this activity.
How would you make a dynamic graph like this one?
Resources & Description
Reminder of Transformations
Here are two Geogebra applets that should remind you of some of the transformations of functions.
For each graph, enter the correct amounts in the input boxes so that the red curve moves and lies on top of the dotted black curve. Create another question by pressing refresh 
. Repeat at least 5 times until you are sure you fully understand the transformation.
Translating
Stretching
The Graphs
Here is the main activity. All of these graphs are produced by plotting a ‘family’ of trigonometric functions. Can you produce these graphs on Geogebra? Your graphs must look identical to the ones in the questions, although you don't need to worry about getting the colours exactly the same! You can record your results by copying the images into the following 
Trig Family Student Answer Sheet and completing the table to show the equation and parameter you used.
You will probably need help getting started with Geogebra for this so a 
help video is provided at the bottom of the page.
Wave 1
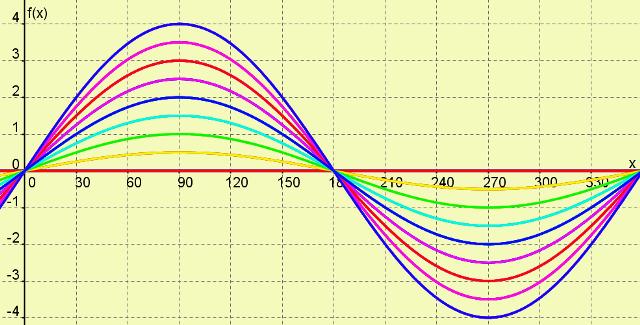
Wave 2
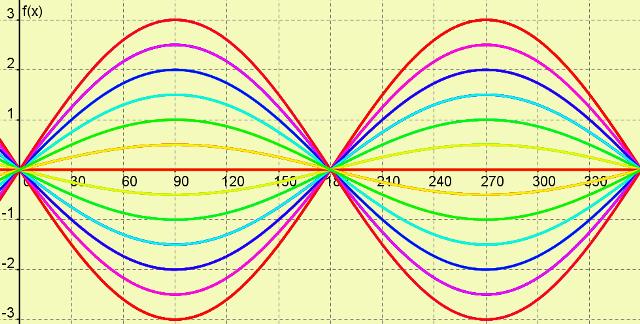
Wave 3
Wave 4
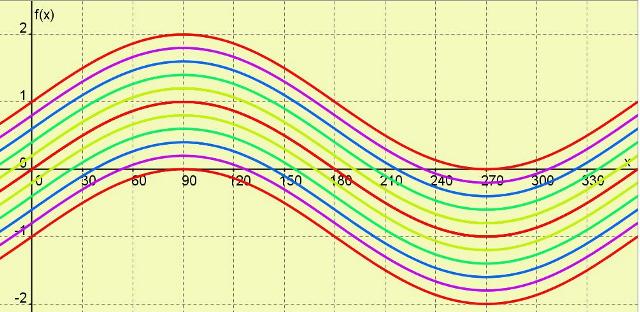
Wave 5
Wave 6
Wave 7
Wave 8
Here's a tricky one to finish with. A point has been placed on the local maxima of the funcions to help you see the two transformations.
Question 9
Your turn! Can you produce a lovely image of your own?
Help Video
Watch this video if you need help in knowing how to produce these families of graphs using Geogebra.