Proof - Pythagoras' Theorem
'Always build bricks on solid ground!'
Would you build a house on sand? Hopefully, not! In mathematics, just like the construction industry, we like to be sure of our foundations before we build. We will only lay the first row of bricks when we are sure of our foundations, we will only build the second row when we are sure of the first row … Imagine if one of those first bricks was a bit wobbly. The whole thing might come tumbling down! We really don't want that to happen. In mathematics we can only be sure of our previous row of bricks by ‘proving’ them. Once we are sure it is solid, then we can move on. Here’s a chance for you to try out your proving skills with Pythagoras’ Theorem. Like good puzzles, proof can be fun!
Description & Resources
1. Students should be familiar with Pythagoras' Theorem. An applet is provided as an aid to memory.
2. A 
cut-up puzzle is included to get the students in the right frame of mind for the later proofs. Getting the students to record their demonstrations is strongly recommended. See video of an example.
3. Three alternative proofs are provided. For each proof a specific numerical example is given to work through to allow the students to understand the process required. Students easily move on to the general case provided they have the neccesary algebraic skills (expanding double brackets and simplifying is the only pre-requisite). If confident, students can try the proofs without the scaffolding.
4. An example of student work is given.
1. What you already know
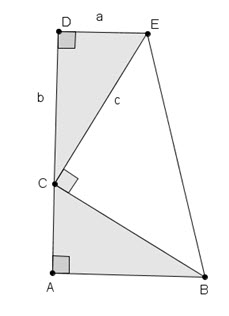
You should have already discovered 
Pythagoras’ Theorem
a² + b² = c²
This 
applet might help you visualize this theorem
2. Demonstration
Cut out the following shapes to show that the theorem is true for the following right angled triangle. Click on the image below to download the file.
Teacher Tip! A great way to provide a record of the students’ work here is to get them to video their demonstration. Here’s an example of a video made by some students of mine.
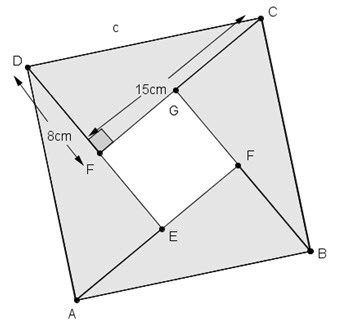
3. Three Proofs
Here's where the action really starts. The images above give a clue to the proofs. The first file provides some structure so that students can work through the proofs with scaffolding. The second file gives no clues. A mixture of the two could be given. Click on the images below to download the files.
Easier - support provided
Difficult - no support
Example of Student Work
This might give teachers an idea of what students are capable of producing.
