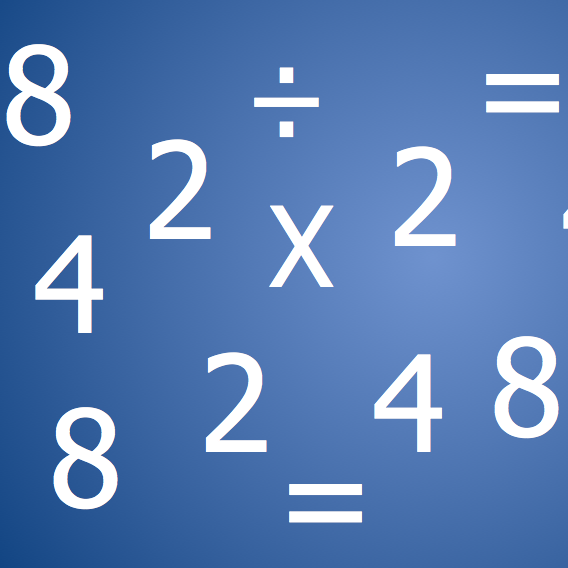| Skewey Squares |
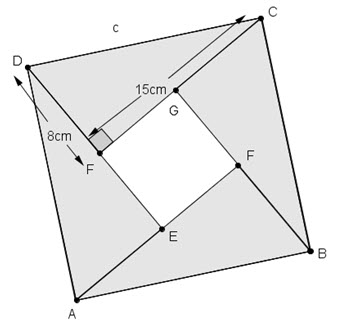 | Time: 1-2hrs Proof is a hugely significant part of mathematics. This activity is an ideal first experience of proof for students since scaffolding is provided: a cut-up activity first allows them to get the feeling for a demonstration of Pythagoras’ Theorem; this is followed by 3 different proofs. The only requirement is that students can find the areas of simple shapes and expand and simplify double brackets. A great introduction to the beauty of proof! |
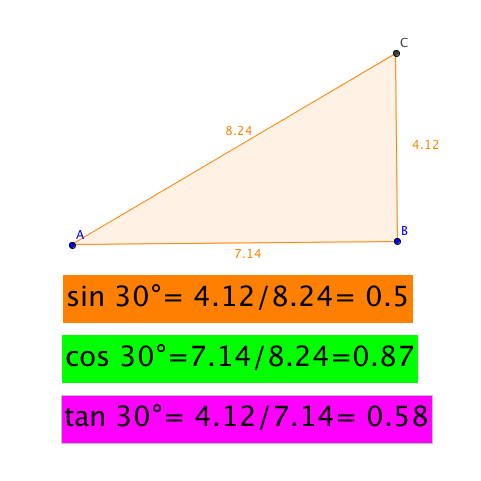
 | Time: 1.5 - 2 hrs This investigation gets students to discover the three trigonometric ratios for right-angled triangles. Dynamic geometry software replaces a classic pencil and paper method for constructing and measuring sides in triangles. Conjectures about ratios are quickly made and tested. |
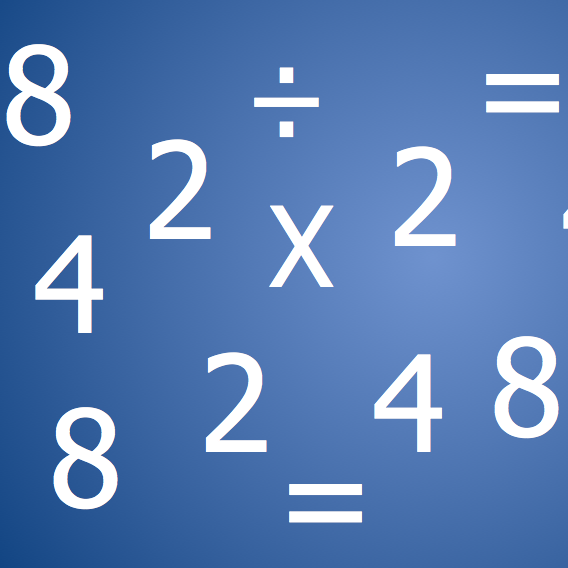 | Time 1hr This activity is all about helping students to understand how to solve right-angled trigonometry problems. The activity encourages students to make 'correct statements' about the situations/diagrams given and become fluent in re-arranging them to make unkowns the subject and ths solve the problem. Students can do this on their own computers or it can be done from a central computer as a whole class activity. |
 | Time: 40mins This short activity asks students to calculate the height of a water powered rocket. This practical lesson gets students out of the classroom and gives them a genuine application of right-angled triangle trigonometry. It is also a great opportunity to explore error bounds. You may even wish to embark upon a joint project with the science department at your school. |
 | Time 1hr This activity is designed to help students solve trigonometry problems by encouraging them to 'Speculate' about what might be possible. Students are asked to state different truths or complete different equations for a given diagram without being told what to solve for. Having completed the equations they are asked to think about which of them is most useful for solving for a particular variable. So often students feel that they must know 'the right thing to do' before they proceed and are afraid to try things out to see what happens. Yes, it is possible to learn how to recognise certain types of problems but it is equally important to learn that problems can be solved by trying to use the different pieces of knowledge you have to make new ones. The sine rule and cosine rule can both be applied to any given triangle it is just that often only one of them generates an equation that can be solved. We can either learn to spot types of problems or to speculate with both. In practice, one often leads to the other and then we are better equipped to solve more problems. |
 | Time 1hr Use dynamic geometry and the fundamental principles of trigonometry to construct and program a trig ratio calculator. The essence of this activity is in students constructing their own. The logical steps required to do so involve real enquiry in to the nature of trig ratios. The result is really pleasing! |
 | Time 1h: This practical activity gets students to make a simple theodolite and use it to make measurements around the school grounds. It’s a great application of the Sine Rule. If students have thought and questioned you about why learning trigonometry is useful then this is the activity for them! They will have no doubt seen surveyors on building sites using digital theodolites on tripods and perhaps wondered what they were doing. This activity gets them to act as surveyors to find the distances between different positions. |
 | Time 1hr: A simple activity designed to get students to reach for their knowledge of triangle geometry. Pythagoras's theorem, SOHCAHTOA, Sine rule and Cosine rule. The activity provides an excellent opportunity for giving meaning to and practising these concepts. |
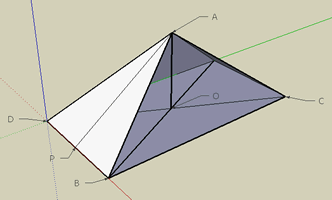 | Time 1-2 hrs. This activity uses technology to help students with the notoriously difficult idea of working with 2D planes within 3D situations and thus solve problems with trigonometry in 3 dimensions.Google Sketchup is a simple and clear visual aid that encourages students to literally look at the problem from a different angle. The medium is both helpful and engaging and lends a dynamic reality to a 3 dimensional object that can't really be achieved with paper! This activity is best done with students at computers, but it can be done all together from the teachers computer if technology is not available. |
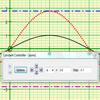 | ATime 1-2 hrs Using Autograph or the free Geogebra or Microsoft Maths 4.0, students investigate the functions of the sine and cosine graph. Students record the key, defining points in a pre-prepared table: coordinates of the maximum and minimum and x-intercepts, as they change different parameters using the constant controller or sliders. Without technology, students then have to predict these key points for different functions. |
 | Time: 30mins-1h. Students use geometry software to model wave pictures from real-life objects and situations. In doing so, students will investigate the effects of the coefficients for sine and cosine waves e.g. y = a cos[b(x-c)]+d asking themselves: “What Changes?”, “What Stays the Same?”. No software is required |
 | Time 1h This activity introduces sine and cosine graphs using the video of the construction of a Ferris wheel that demonstrates the link with triangles. Students then sketch the graph of their movement on the Big Wheel. The aim is to link the sine and cosine ratios to a circle. Students use calculators to plot the graphs exactly (spotting symmetries to save them calculation time!). VM also available. |
 | Time: 1h. This activity helps students see the connection between mathematics and music. Students see the shape of music (pure tone sound appears as trig functions) thanks to sound recording software ( Audacity). No need to install the software, as short videos and images are ready to use. Students would be expected to have seen the graph of a sine curve before, and have some understanding of transforming graphs. |
 | Time 1.5 hr + This activity gets students to produce families of trigonometric functions (like the one on the right) using dynamic geometry software. By exploring the effect of changing parameters they really get a deep understanding of the properties of the main transformations: translations and stretches. Get ready for "Oos and Ahhs"! |
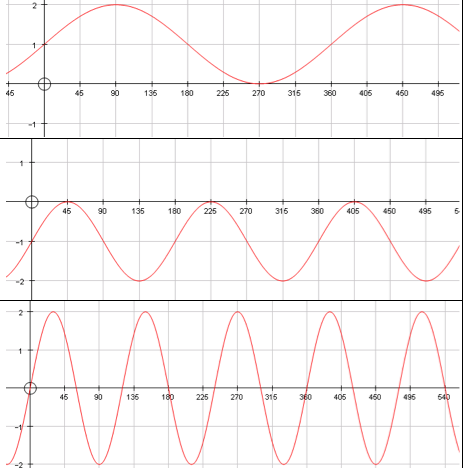 | Time 30-40 minutes. Match the waves with their functions! The discussions and reasoning that take place during this type of activity can be incredibly valuable and effective. It is a simple idea, but so often the simple ideas can be the most effective. It is also a nice alternative to a traditional exercise. When well practised, this is not a desperately difficult concept and it can be very satisfying to be able to quickly make the link and either deduce a function from the graph or the other way round. This simple activity lends itself to group work and presents the kind of challenge that usually engages students |
