Prime Pictures
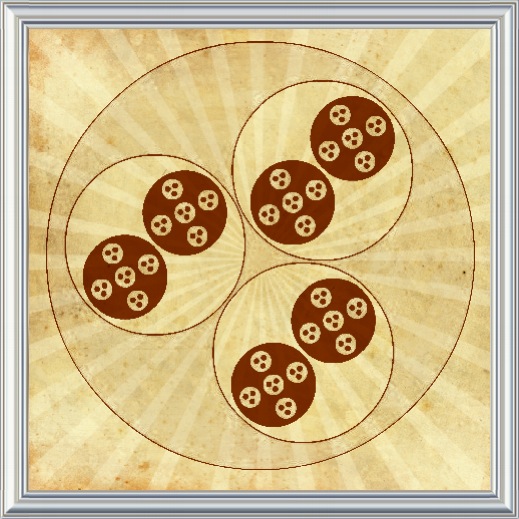 'Decode these pictures and unravel the power of prime numbers'
'Decode these pictures and unravel the power of prime numbers'
- Page under construction and review -
Our number system is so jam packed full of patterns and mysteries that we could easily spend a lifetime exploring them all. Indeed many people do! One angle to take is to visualise numbers in different ways and this activity is all about visualising numbers in a particular way. The images below are all taken from the wonderful 'Primitives' manipulative, linked at the bottom of the page (looking at it now would rather spoil the activity, but I recommend it afterwards).
There are three activities here based on 'cracking this code' and then a fourth to see if you can use the code to start representing your own numbers. It is hard to say much here without giving the game away, but here a few questions you could ask...
- What is the significance of the number of different sized circles used?
- What is the significance of the colours used?
- What do certain types of numbers have in common in the way they look? How can different pictures represent the same numbers?
- How many different ways are there of representing the same numbers?
Resources
The tasks are in no particular order and each one involves working with a group of 30 pictures. Good luck!
![]() 1 - 30 - These are the numbers from 1 to 30. Can you figure out which is which? Read the instructions given on the sheet.
1 - 30 - These are the numbers from 1 to 30. Can you figure out which is which? Read the instructions given on the sheet.
![]() How many numbers? Here are 30 different images, but how many numbers do they represent and how many times does each appear?
How many numbers? Here are 30 different images, but how many numbers do they represent and how many times does each appear?
![]() 30 Numbers - These are 30 numbers between 1 and 100. There are some clues to go with them to help you figure out which is which.
30 Numbers - These are 30 numbers between 1 and 100. There are some clues to go with them to help you figure out which is which.
![]() Crack the code and make your own! Make sure you understand what is going on here and then make some of your own pictures.
Crack the code and make your own! Make sure you understand what is going on here and then make some of your own pictures.
Below is a screen shot of the first sheet to give you an idea.
.jpg)
Description
- Teachers will need to decide which of the three activities to use and in which order. They could be used to differentiate with the third task probably being the more difficult.
- The main focus for the activity is the discussion associated with each set of pictures. Make sure that observations and conjectures are shared and recorded along the way.
- Working out which number is which is only half of the job, to make new pictures students need to have unlocked the code.
- Once cracked, students should make their own pictures. There is a real opportunity to be creative here and move away from circles.
For Teachers
This activity is based on the wonderful ![]() 'Primitives' manipulative. Like so many wonderful things out there, I really wanted to build an activity around it to help students draw on their curiosity to understand the pictures, rather than simply show them the outcome. As a teacher I would want to show this at some point during the lesson, but not at the beginning, otherwsie too much is given away too soon.
'Primitives' manipulative. Like so many wonderful things out there, I really wanted to build an activity around it to help students draw on their curiosity to understand the pictures, rather than simply show them the outcome. As a teacher I would want to show this at some point during the lesson, but not at the beginning, otherwsie too much is given away too soon.
The real richness of this activity is not in the solutions, but in the discussions that lead to them. Investigating the role of the colours, the number circles used, the different ways of making the same numbers and so on, should help students explore the properties of the numbers themselves. It is lovely if students realise the role of prime numbers themselves and start making associated conjectures. Equally, you might conclude that square numbers were always the same colour and then find a counter example. You might print the worksheets in black and white and make it more difficult! There are so many possible questions and angles here that it is quite difficult to predict how the lesson will go.
It is nice if the lesson finishes with the making of images that can be used for great display and memory aid!
Here are the ![]() Prime Picture Numbers and Solutions. For the second and third exercises you might choose to help students by telling them what the numbers are.
Prime Picture Numbers and Solutions. For the second and third exercises you might choose to help students by telling them what the numbers are.
A note on edible extensions!
I have discovered that there is potential in the idea of reproducing these diagrams in the form of cakes! See this blog post about how we took edible prime pictures to a local mathematics festival! Can you tell what these numbers are?





