Logarithms: What are they? History & Applications
Using only pencil and paper work out 984 876 543 210 x 875 622 375 933. You have 2 minutes . . . go!
 Have you worked it out yet: 984 876 543 210 x 875 622 375 933 ? Compare methods in the class - have we all used the same method? Now compare your answers, are they all the same?
Have you worked it out yet: 984 876 543 210 x 875 622 375 933 ? Compare methods in the class - have we all used the same method? Now compare your answers, are they all the same?
Most people tend to make a mistake at some point in that calculation (maybe you did too?) and two minutes isn't enough time (for ![]() most people) to complete it! Another solution is required.
most people) to complete it! Another solution is required.
Overview of this Activity
Option1: Mechanical Calculators
There was a time when the German produced Schubert calculator was high-tech (late 1950s early 1960s). I have one of these mechanical calculators in my classroom. Challenge: can you work out/find out, how it works and be ready to show the class next lesson?

Option2: Log Tables (turn every number into a power of TEN)
For this you’re going to need your laws of indices/exponents (this activity may help remind you: Prime and Powers Investigation). Can you remember what: 2.54624 x 2.54628 = ______________ ?
Hopefully you remember your “laws of indices/exponents”? Write a quick summary on a sheet of paper.
Resources
Using Log Tables
We’re going to use a simple example, to illustrate how to use log tables ("zoom in" to enlarge the table below) effectively to do: 2.07 x 2.08.
a) Use the “Log Table” below to find what power of 10, 2.07 and 2.08 are equal to (then see the instructions below for the next steps).
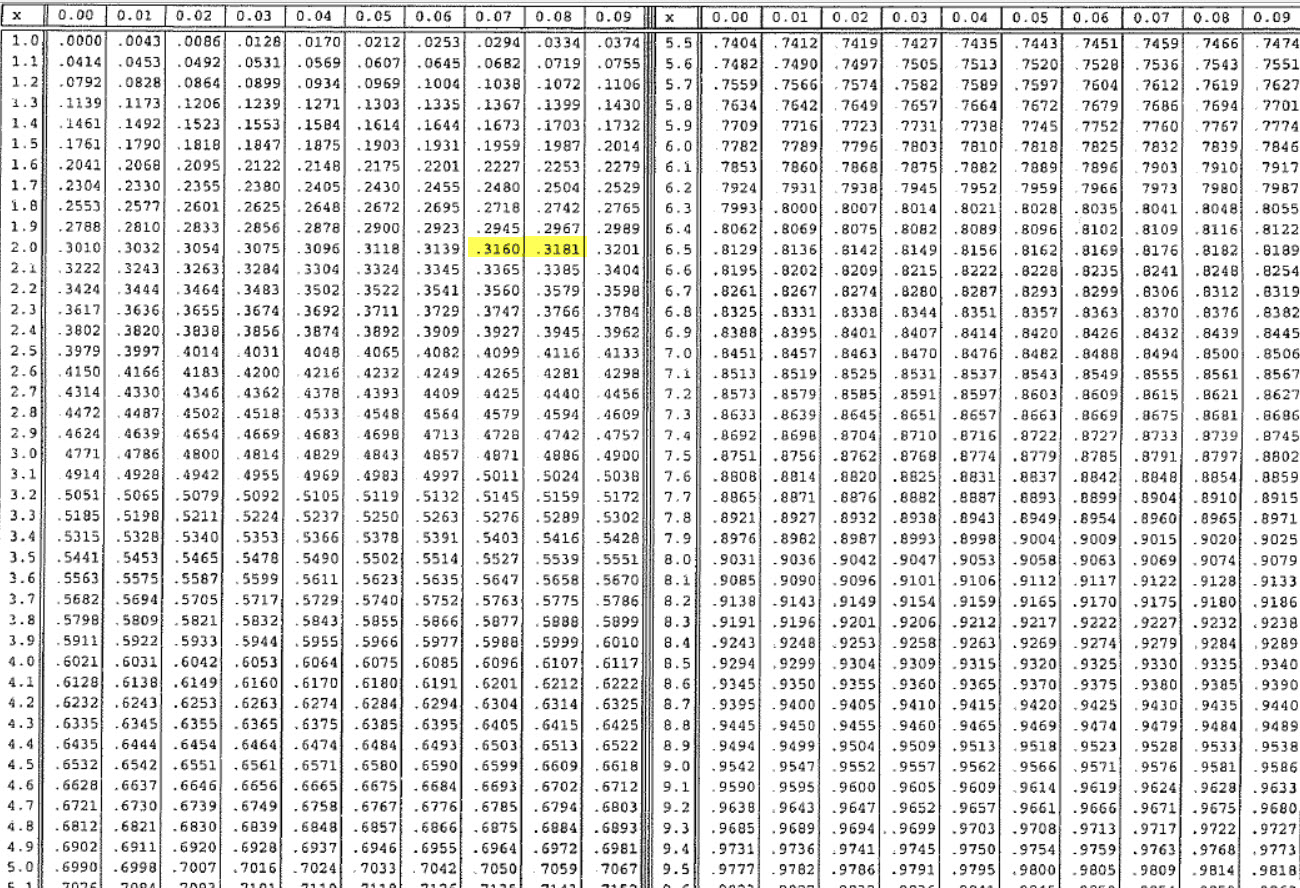
http://math.ucsb.edu/~myoshi/logtable.bmp
- Add these powers/exponents.
- Now find the sum of these powers in the table and read off what number this new power corresponds to.
- Is the answer the same as what you get if you do do 2.07 x 2.08 using a long multiplication method? Test it: by typing in 10^the sum of the power of ten for 2.07 and 2.08, into your GDC.
b) Try using the log tables again to find out what 2.37 x 4.19 is equal to (and how could you use this to work out 237 000 x 4 190 000 or 0.00237 x 0.000 0419 ?).
c) Repeat this process three times, each time using numbers in the above table, and then adding the powers and finding what number this corresponds to. Check your answers using your calculator.
Note: If you're interested in understanding how these log tables were calculated in an era before calculators, see the "History of Logs" section below.
With Calculators, why do we still use logs today?
Plot the data below in any spreadsheet graphing software of your choice: Geogebra, Autograph, TiNspire or Casio, Desmos etc. You can copy and paste it directly from the below spreadsheet:
What problem do you notice?
How might "logarithms" help you to resolve this problem?
Your ![]() divisibility tests may help. Log tables use powers of 10, but you could equally use powers of 2 or 5 or 9 . . . or any number you prefer.
divisibility tests may help. Log tables use powers of 10, but you could equally use powers of 2 or 5 or 9 . . . or any number you prefer.
You understand what a Log is? Put your knowledge to the test:
Test 1: Log(100) is asking a question - if you can translate the mathematical notation and ask yourself the question, the answer becomes obvious. Translate the mathematics!
Log(10 000)=
104 = 10 000
Log(0.001)=
10-3 = 0.001
Log(100)=
102 = 100
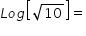
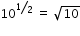
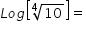
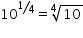
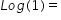
Any number to the power of zero = 1
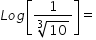
Negative powers are the "reciprocal" of the positive power
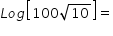
For all questions from here onwards, tick ALL the answers that are correct (there may be more than one).
Convert both 100 and 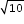 into powers of ten. Then when you multiply powers you know to add the powers.
into powers of ten. Then when you multiply powers you know to add the powers.
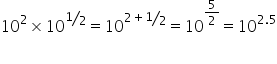
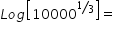
Laws of powers/indices: multiply powers when raising one power to the power of another e.g. (10a)b = 10ab
Log[10m]=
The power of 10 is equal to 'm' in this question
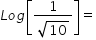
Negative powers are the "reciprocal" of the positive power
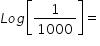
This is the same question as Log(0.001): 0.001 = 10-3
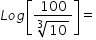
When you divide powers you subtract them: 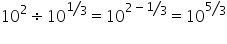
OR multiplying powers you add them: 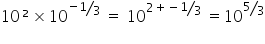
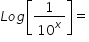
Negative powers are the "reciprocal" of the positive power.
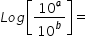
When dividing powers, you subtract the powers.
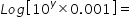
Convert both into a power of 10 and then add the powers: 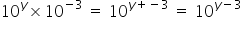
Test 2: Logs NOT to the base 10
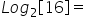
There could be more than one answer in the questions that follow.
24=16
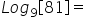
9²=81
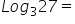
33=27
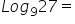
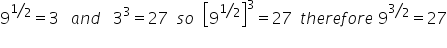
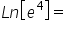
Ln means log to the base 'e' where 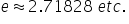
For the following questions you need to find the value of the letter
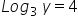
34 = 81
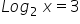
23 = 8
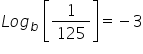
5-3 = 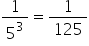
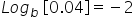
5-2 = 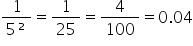
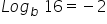
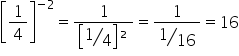
Applications of Logs
Gapminder (UN data)
Many of the graphs concerning human well-being, from the Gapminder website, use a logarithmic scale. Can you explain why the x-axes below is a logarithmic scale but not the y-axes?

The Richter Scale
You can find a range of "Earthquake" apps on android and itunes that will offer you alerts on earthquake activity around the world, as well as some offering you data on earth tremor activity detected by your phone. Here's a couple to get you started:
<
For an explanation of how the Richter scale is calculated, ![]() watch the first three minutes of this video from the Khan Academy
watch the first three minutes of this video from the Khan Academy
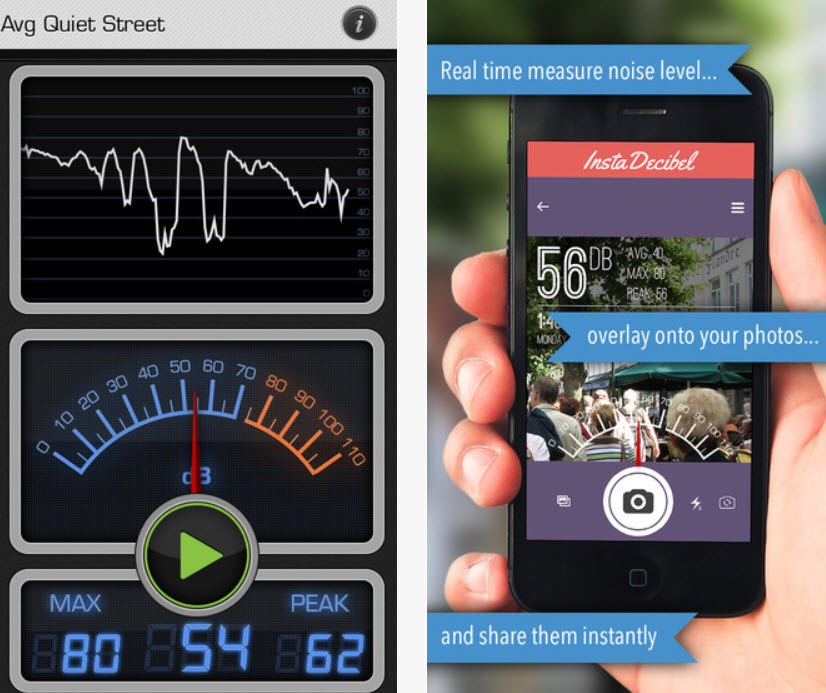
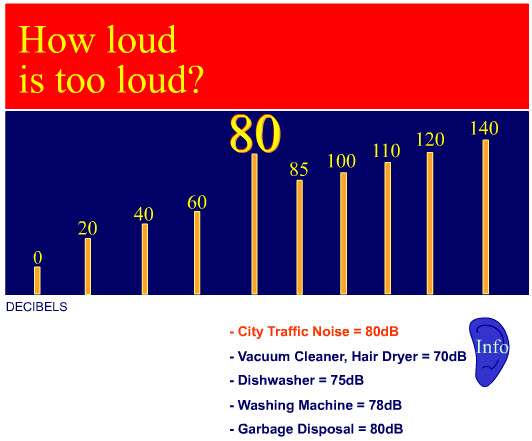
The Decibel scale
There's a range of decibel meters available both on android and itunes, that provide great opportunities for further investigation and exploration of logarithmic scales and cross-curricula (DT, Science & Geography) projects:
iTunes "Decibel 10th" Android "Sound Meter"
Click on the images below to get a feel for the noise level to expect for a given number of decibels:
Modelling very varied Data
In the Influenza pandemic graph below, the y-axis is a logarithmic scale – what base is it using?
What does each unit on the y-axis represent?
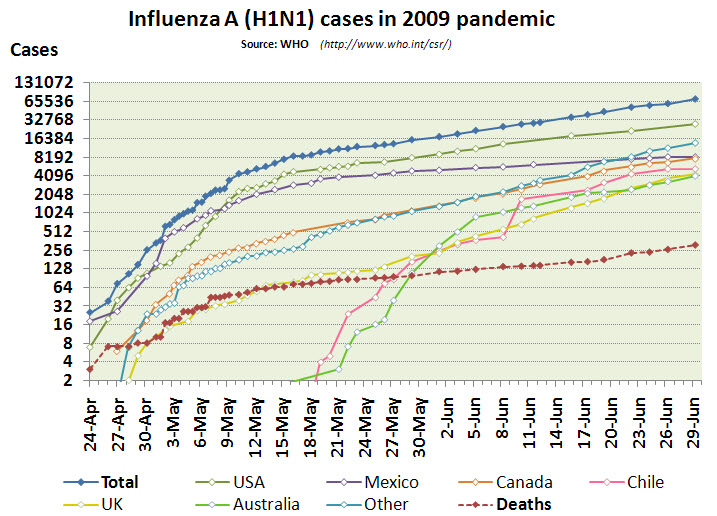
http://en.wikipedia.org/wiki/File:Influenza-2009-cases-logarithmic.png
History of Logs
Two fantastic articles from the "Math Forum: Asks Dr Math" - to access them you will need to first quickly set up your FREE account with the National Council of Teachers of Mathematics (USA), then click on the links below :) :
![]() How were the first log tables calculated (given there were no calculators)?
How were the first log tables calculated (given there were no calculators)?
Description
- The long calculation: 984 876 543 210 x 875 622 375 933 provides a first hand experience for students of the need for a simpler way to multiply (and divide etc.) big numbers. The log table activity then gives students a feel for how time-saving, pre-calculator age, these log tables were. It's also a great opportunity for students to talk with their parents and maybe even work out how a slide rule works (good revision of AP and GP sequences!).
Why do we still use logarithms today? Students copy and paste in some sample data that illustrates the difficulties of plotting very varied data.
These opening activities provide students with a good conceptual grasp of what logs are. It's time to test their understanding with a couple of online quizzes.
As a class, or individually, students/the teacher, may want to investigate modern applications of logarithms and/or the history of the development of logarithms with their classes. There are some great investigations students could do using apps such as android's
Sound meter and iphone's
Decibel 10th. For earthquake apps, try iphone's
iFeltThat or android's
Earthquake Network.