Lisbon - November 2011
Introductory Geogebra

Objectives - To support workshop participants to get to grips with geogebra software and demonstrate its uses in the mathematics classroom.
Aims - Participants should observe potential, get practice, be inspired to use it in the classroom!
Content - Learn the basics of creating geometrical figures, measurement and calculation; coordinate geometry and functions for elementary and advance topics.
Why Geogebra?
Free, attractive interface, relatively easy to use yet powerful.
Large active and supportive community geogebra forum. Twitter users should check out #geogebra
Huge catalogue of ready to use applets geogebratube
Some of my favourite 'sketches'
Downloading
Requirements - need java installed and ensure that your browser is java enabled.
- ![]() Install and start GeoGebra on your computer.
Install and start GeoGebra on your computer.
Applet start - Open a fully functional GeoGebra applet in your web browser. Nothing will be installed on your computer. Good for working on unfamiliar computers provided you have an internet connection – should work on any computer!
Geogebra 4.2 Beta version with CAS
Geogebra 5 Beta version with 3D
Getting Started
Windows, Views, Toolbars
Objects - free, dependent, semi-dependent
Options - point capturing, labelling, font size
Sliders & Variables
Skewey Squares an activity to help students discover Pythagoras's Theorem. Let's create a manipulative that will take the labour out of the task.
Equable shapes - use sliders to change the length of a polygon and change the number of sides of an n-polygon.
Watch the following video for a reminder of the task
Need some help with Geogebra? Watch the following
Challenge - Inscribed Polygon
This is an extension task in which you will have to use the slider creatively. The task is to produce an inscribed polygon to get an approximation for pi. Watch the following video to find out what to do.
Transformations
Geogebra deals with the obvious transformations in a simple manner. You can embed them in webpages, wikis & moodle pages Naure's symmetry.
Sliders and animation can bring these transformations to life.
You can use screencam demonstration to ask animated questions. Try some of the following
Dynamic Text
There are a number of ways of creating dynamic text. Here I will show a Pythagoras' Theorem applet to show how useful it can be.
Introduction to Trigonometry - Here is a figure to help students explore right-angled triangles. Double click to open the geogebra file. Add some dynamic text to show the ratio of opposite divided by hypotenuse. Add some more text to show sin(angle).
Plotting Coordinates & Graphs
The following applet shows how geometry, algebra and graphing can be combined in the same geogebra applet
Dancing Quadratic Can you produce the following graph?
Find some pictures and try to model the function e.g. Modelling Quadratics
Looking for a challenge? Try to produce a Unit Circle like the one below.
Clue: to force Geogebra to show the correct angle as the triangle travels around the circle, try rotating a point from (1,0 about the origin through your slider angle and creating a sector (the shading helps the eye). I have used two graphics windows, but this can be done in one if you use radians (in my opinion the effect is not as good!)
Inputing Commands
A full list of commands are available on Geogebra help
Here is a file that shows the gradient of the exponential function using the command Derivative[
You can improve this last file by showing the slope and using trace to plot the gradient function 'manually'
You can create Riemann approximations to find the area under a graph - a useful investigation for discovering integration?
Here I used the command Integral[
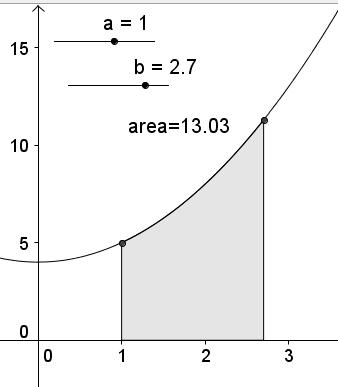
Explore some other commands on Geogebra and use your imagination to produce an applet.
Extras
Parabolas. Ana Maria Dianderas asked about plotting parabolas from 3 points. Geogebra plots parabolas from their definition: the locus of points equidistant from a point (focus) and a line (directrix). Try it! It is more of a challenge to plot a parabola from 3 points (here's an applet that does that), but I recommend this lovely investigation which looks at making the line a curve Generalising parabolas (look at p13 & 14).

